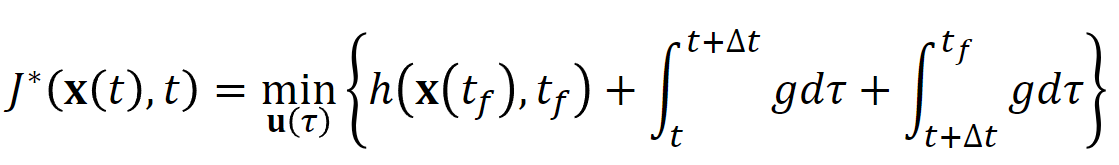Optimal Control은 Dynamic Control System에서 Goal state와 Current state의 error를 Performance measure(Cost function)로 표현하고 이를 최소화하는 최적의 Control variable, 'u'를 찾는 문제
State Equation, Performance measure(J) 정의
- mxm Square Matrix H, Q는 positive semi definite
- H,Q가 모든 벡터 x에대해서 transpose(x)*Hx>=0
- nxn Square Matrix R positive definite
- R가 모든 벡터 u에대해서 transpose(u)*Hu>0


→We can minimize J
Principle of optimality, Taylor Expansion을 이용해 Performance measure을 Partial Differential Equation으로 정리
- Recurrence Equation을 편미분 형태로 표현하고 best control option을 선택하기위함
- Hamiltonian 정의
Hamiltonian을 최소화 하는 입력u*를 찾고 Hamilton-Jaconbi-Bellman Equation에 u*를 대입
- Final boundary condition으로 부터 J*의 기본적인 form을 추측해볼 수 있음
Riccati differential equation으로부터 Algebraic Riccati Equation
'maengkyun > Robotics' 카테고리의 다른 글
| Alexmos Simple BGC:: AS5048A(AS5048L) Encoder Connection (2) | 2022.11.02 |
|---|---|
| Limit-Cycle 특성을 이용한 항법 (1) | 2022.10.18 |
| Optimal Control - Dynamic Programming(1) (0) | 2022.07.31 |
| RRT:Rapidly Exploring Random Tree 경로 생성 알고리즘 (0) | 2022.07.14 |
| [Kalman Filter] SORT(Simple Online and Realtime Tracking) (0) | 2022.06.14 |